树上换根dp

换根dp: 换根dp往往需要处理去掉一个子树这样的问题，我们可以使用前后缀和的方法来优化复杂度

Problem - 543D - Codeforces

题意：一个国家有n个城市，n-1条道路，保证是一棵树，起初所有道路都是破旧的。对于每个点x，求以x为首都的时候修建道路使得成为完美国家的修建方案数。对于完美国家的定义是：从首都出发，到达任何城市的最短路上最多只有一条破旧的路。

Sol：考虑换根dp。首先先求出1为首都的答案。$dp[u]表示u的子树的方案数，考虑一个具体儿子v。如果u-v这条路是被修复了，则方$案数是$dp[v]$。如果如果u-v这条路是破旧的，则v的子树的路必须全部被修复，只有唯一方案。

转移：$dp[u]*=dp[v]+1$

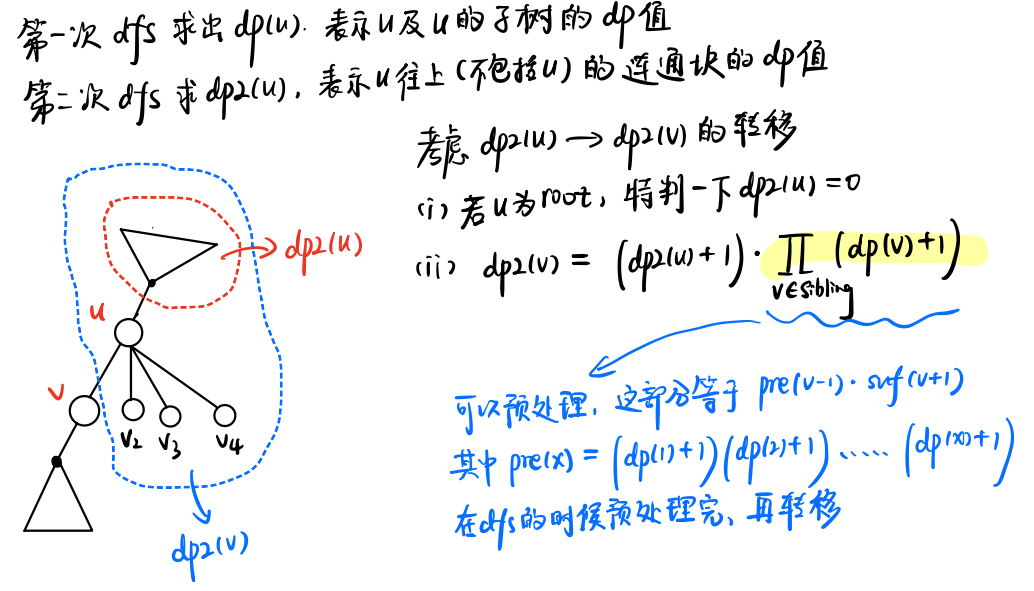
考虑换根：进行第二遍dfs，一般是先计算向上的答案，再递归进去。考虑原先父亲对自己的贡献，up[v]表示在以v为根的情形下，考虑u的部分子树（以v为根的方向）的贡献。

具体哪部分？答：之前是u祖先现在是u子树的方案数。

• $u = root$ $up[v]*=1$
• $u \ne root$ $up[v]*=(up[u]+1)$

进一步考虑剩下那部分，也就是之前是u的子树现在也是u子树。一个简单的想法你可能会发现也就是原先的儿子们dp值乘积贡献去除掉v的贡献，也就是$dp[u]*inv(dp[v]+1)$。但是首先出题人可以要答案取模的质数不是质数，逆元难度增加，进一步即使是质数，如本题是$1e9+7$，但是也容易构造成取模为0的数据出现，导致不存在逆元，计算出错。

• 考虑一个trick，我们只需要维护前缀贡献，后缀贡献，假设v是第i个儿子，去除v的贡献就是$pre[i-1]*suf[i+1]$，预处理这个就是可以$O(1)$计算这部分了。
• 实现的细节：对于自己父亲是根的时候，根不存在父亲，计算up的时候需要特判

void solve() {
    int n;
    cin >> n;
    vector<int> dp(n + 1), up(n + 1);
    vector<vector<int>> e(n + 1);
    for (int i = 2; i <= n; i++) {
        int x;
        cin >> x;
        e[x].push_back(i);
    }
    vector<vector<int>> pre(n + 1), suf(n + 1);
    auto dfs = [&](auto self, int u) -> void {
        vector<int> tmp;
        dp[u] = 1;
        for (auto v : e[u]) {
            self(self, v);
            dp[u] *= (dp[v] + 1);
            dp[u] %= mod;
            tmp.push_back(dp[v] + 1);
        }
        int sz = tmp.size();
        pre[u].resize(sz + 1), suf[u].resize(sz + 2);
        pre[u][0] = 1;
        suf[u][sz + 1] = 1;
        for (int i = 1; i <= sz; i++) {
            pre[u][i] = pre[u][i - 1] * tmp[i - 1];
            pre[u][i] %= mod;
        }
        for (int i = sz; i >= 1; i--) {
            suf[u][i] = suf[u][i + 1] * tmp[i - 1];
            suf[u][i] %= mod;
        }
    };
    dfs(dfs, 1);  // 以1为根的答案
    vector<int> ans(n + 1);
    up[1] = 1;
    auto cal = [&](auto self, int u) -> void {
        int sz = e[u].size();
        for (int i = 1; i <= sz; i++) {
            int v = e[u][i - 1];
            up[v] = pre[u][i - 1] * suf[u][i + 1];
            up[v] %= mod;
            if (u > 1)
                up[v] *= (1 + up[u]);
            up[v] %= mod;
            self(self, v);
        }
    };
    cal(cal, 1);
    ans[1] = dp[1];
    for (int i = 2; i <= n; i++) ans[i] = ((up[i] + 1) * dp[i]) % mod;
    for (int i = 1; i <= n; i++) cout << ans[i] << " ";
}