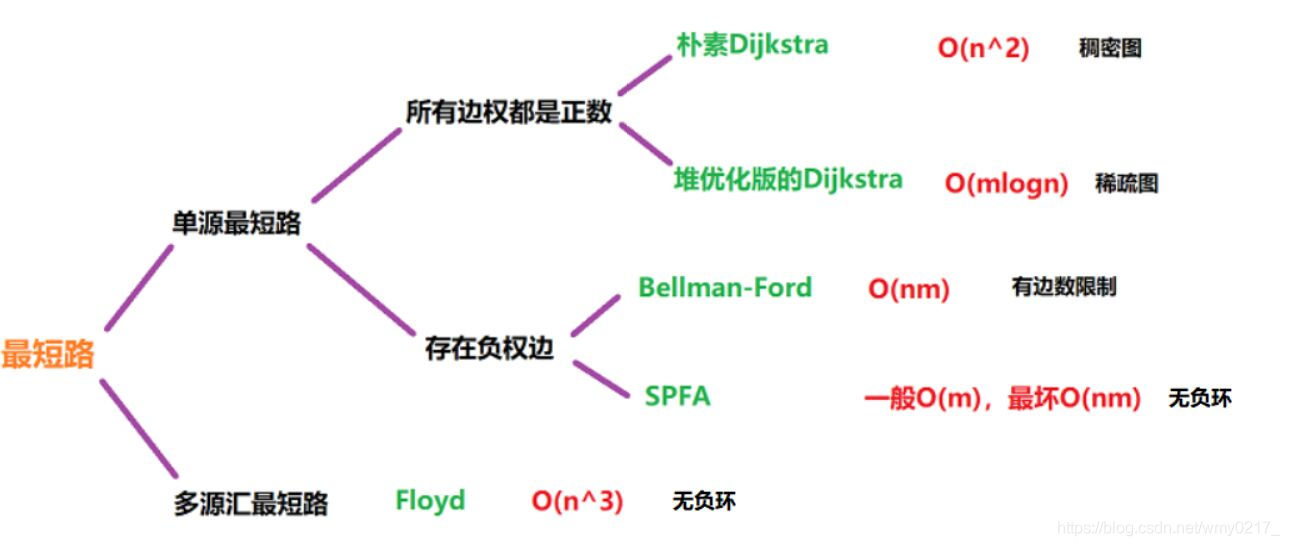
单源最短路： 求一个点到其他点的最短路
多源最短路： 求任意两个点的最短路

稠密图用邻接矩阵存，稀疏图用邻接表存储。

稠密图： m 和 n2 一个级别
稀疏图： m 和 n 一个级别

朴素dij：

int n,m,s,a,b,c;
const int N=100010;
struct edge{int v,w;};
vector<edge> e[N];
int d[N], vis[N];

void dijkstra(int s){
  for(int i=0;i<=n;i++)d[i]=inf;
  d[s]=0;
  for(int i=1;i<n;i++){//枚举次数
    int u=0;
    for(int j=1;j<=n;j++)//枚举点
      if(!vis[j]&&d[j]<d[u]) u=j;
    vis[u]=1; //标记u已出圈 
    for(auto ed:e[u]){//枚举邻边
      int v=ed.v, w=ed.w;
      if(d[v]>d[u]+w){
        d[v]=d[u]+w;
      } 
    }
  } 
}
int main(){
  cin>>n>>m>>s;
  for(int i=0; i<m; i++){
    cin>>a>>b>>c;
    e[a].push_back({b,c});
  }
  dijkstra(s);
  for(int i=1;i<=n;i++)
    printf("%d ",d[i]);  
  return 0;
}

堆优化版dij

//堆优化Dijkstra 

#define pii pair<int,int>
struct edge {
    int v, w;
};
vector<int> dijs(vector<vector<edge>>& e, int s) {
    priority_queue<pii, vector<pii>, greater<pii>> q;
    vector<int> d(n + 1, (1LL<<31)-1);
    vector<bool> vis(n + 1);
    d[s] = 0;
    q.push({d[s],s});
    while (q.size()) {
        auto t = q.top();
        q.pop();
        int u = t.sec;
        if (vis[u])
            continue;  // 再进队就直接跳过
        vis[u] = 1;    // 标记u已出队
        deb(u);
        for (auto [v, w] : e[u]) {
            deb(v,w);
            if (d[v] > d[u] + w) {
                d[v] = d[u] + w;
                q.push({d[v], v});  // 小根堆
            }
        }
        
    }
    return d;
}

#最简单处理带负权边的最短路

void floyd()
{

    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
init(){
 for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;
}
存边方式： d[a][b] = min(d[a][b], w);
# 如果是无向边需要加d[b][a]

处理负权边

有边数限制（1 号点到 n 号点的最多经过 k 条边的最短距离。）

const int N = 510, M = 10010;
struct Edge
{
    int a, b, c;
}edges[M];

int n, m, k;
int dist[N];
int last[N];

void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);

    dist[1] = 0;
    for (int i = 0; i < k; i ++ )
    {
        memcpy(last, dist, sizeof dist);//每次只多加一个点，防止串联更新
        for (int j = 0; j < m; j ++ )
        {
            auto e = edges[j];
            dist[e.b] = min(dist[e.b], last[e.a] + e.c);
        }
    }
}

int main()
{
    scanf("%d%d%d", &n, &m, &k);

    for (int i = 0; i < m; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        edges[i] = {a, b, c};
    }

    bellman_ford();

    if (dist[n] > 0x3f3f3f3f / 2) puts("impossible");//即使不连通也可能会被轻微更新，只要在无穷大数量级数说明不可达
    else printf("%d\n", dist[n]);

    return 0;
}

在遇到负权的时候才考虑spfa，很容易被卡

const int N = 100010;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    queue<int> q;
    q.push(1);
    st[1] = true;

    while (q.size())
    {
        int t = q.front();
        q.pop();

        st[t] = false;//可能二次入队，所以要还原。因为入队都是被更新的，所以其要二次更新它能到的点。

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    int t = spfa();

    if (t == 0x3f3f3f3f) puts("impossible");
    else printf("%d\n", t);

    return 0;
}